Remember remainders?

The topic of 'remainders' came up in class today and one of the students was saying how she remembered being  taught in school to just say "remainder 1" or "remainder 2" when a number did not "go" exactly "into" another number in a division problem.

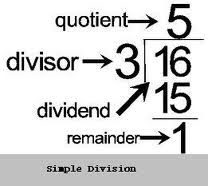
Division, or "dirision" as Lewis Carroll called it, has always been the ugly sister to the other three operations and should never, as math lore clearly states, be attempted any time before fourth grade. I actually once had a third grader say to me "You can't talk about division until we get into fourth grade".  This is all nonsense of course as the picture to the lower left shows. We can do simple division in  first grade
   as long as students understand what it  means.
 
The depressing thing about the top picture is that it illustrates how much attention we used to give to naming the different numbers and how little attention we paid to what was really happening. Think about the remainder in the top picture for a minute. The remainder is clearly 1,  but 1 what? We could even record the remainder as 1/3 or .333333 etc but 1/3 of what would it be?

To answer these questions we need to know the nature of the referents of the numbers. In the lower picture we know these, or at least one, and we can assume the other. The referent of the 7 would be cookies and the referent of the 2 could be children as in "How many cookies would each child get if they shared 7 cookies equally between them?" There would be 1 cookie left over or each child could get 3 1/2 cookies. But, supposing we changed the question? How many children could get 2 cookies each if there were 7 cookies in the cookie jar? The problem would still look the same (7 ÷ 2 = 3 R1)  but this time it would be 3 children and not 3 cookies. What what would the remainder 1 be? It could sort of still be one cookie,  but what if we reported it as a fraction? 3 and a 1/2, or 3.33333 children?